因子分析法构建景气指数模型的探讨

         在市场调研中，我们经常需要向客户提供该公司运营状况及其所在行业整体运行情况等宏观信息，单纯靠财务分析及引用国家行业景气指数已不能满足客户的需求，景气分析的重要性日益突出。
　　 景气分析又称为商业周期分析，主要利用月度或季度经济统计序列资料构建一个景气指数，用以分析和判断经济发展周期性波动所处的阶段（扩张阶段还是收缩阶段、峰点谷点还是景气转折点），找出景气状态发生变动的原因，预测未来经济景气走向，验证和评价政策实施的效果等。
　　本文通过因子分析法构建了一个简单的景气指数模型，该模型适用于行业景气及企业运营状况（行业景气的微观版）方面的简单分析。需要注意的是，在做不同分析时指标应做相应的修整。另外，从以下文中指标的选择上可以判断该指数为一致合成指数，要做更进一步的分析还需先行指数、滞后指数的支持。

　　一、构建前期工作

　　（一）充分了解影响景气的主要因素
　　 影响景气的因素一般可分为内外两种：外部因素主要包括国际形势、宏观政策、宏观经济指针、经济周期、上下游产业链的供应需求变动等；内部因素主要为产品的需求变动、生产能力变动、技术水准变化、人力资源改善及产业政策的变化等。

　　（二）选用适合的指标
　　 景气分析的常用指标可分为两级：一级指标是影响景气的重要因素,二级指标是其细分的结果。一般的常用指标如下:

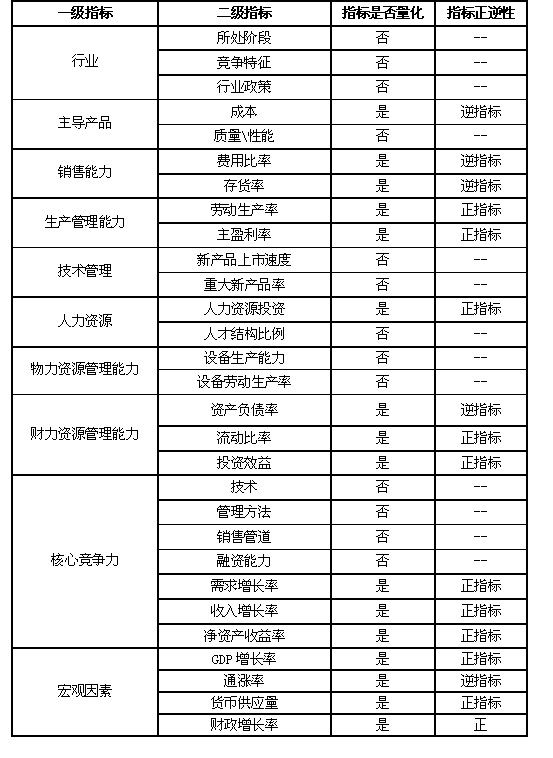
　　以上指标均为通用指标，在具体构建某一景气指数时应依据实际情况增减相关指标。

　　（三）数据预处理
　　 1、异常数据的处理
　　 异常数据是指观测数据的过大或过小的值。异常数据可能只是数据中内在的随机变异性的一种极端的表现，也可能是因为实验过程中出现的操作失误或条件改变所致。对于前一种异常数据，必须给予保留并与其它资料一起参与统计过程。对于后一种数据，必须舍弃或修正。因此，一个过大或过小的值是否是真的异常值，需要首先进行判断，判别的方法是进行检验。如果数据服从正态分布，检验的方法有奈尔检验、格拉布斯检验等。
　　 当正态总体的方差已知时，采用奈尔检验，奈尔检验的统计量为

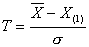    或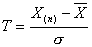

　　当正态总体的方差未知时，采用格布拉斯检验，该检验的统计量为

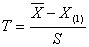    或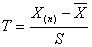

　　式中，S为方差。
　　 当显著性水平和样本的数据个数已知时，通过查表可以得到临界值，当最大或最小对应的统计量大于临界值时，认为该值异常，剔除该值。剔除异常值后，需要对剩下的数据重新进行异常值检验，并重复以上过程，直到没有数据能被剔除为止。
　　 2、逆,适度指标处理
　

    正指标是越大越好,用因子分析法,对于逆指标,适度指标不太适用,一般要将它们化为正指标.对逆指标,选择简单变换,  

    对适度指标,其指标为, , ,假定最适合的值是,偏离越大越不好,因此,就反应了不好的程度,它相当于一个逆指标,于是令
　　
　　 .   即为正指标.

　　3、数据的标准化
　　 对于具有不同级或不同单位的数据，在进行数据统计之前，往往需要进行处理，使资料在更平等的条件下进行分析。目前进行数据处理的方法大致有3种，既标准化、极差标准化和正规化。
　　 (1)标准化
    假设 为原观测值，为数据均值，S为标准差，则标准化后的观测值为

　　(2)极差标准化
    假设为原观测值，为最大值，为最小值为数据均值，则极差标准化后的观测值为，极差标准化以后的数据在－1～1之间。

　　(3)正规化
    正规化的计算公式为

　　二、景气指数模型构建

　　 1、选择因子分析法的原因
　　 要正确反映某一行业或某一企业是否景气，必须从不同的方面进行描述和分析，在众多的分析法中因子分析法有其独到之处，它可以从宗错复杂关系的经济现象中找出少数几个主因子，每个主因子代表经济变量之间相互依赖的一种经济作用，抓住这些因子就可以帮助我们对复杂的经济问题进行分析和解释。因此，本文景气指数的构建采用了因子分析法。
　　 2、因子模型分析法则
　　 因子模型法基本原理及因子分析法的基本思路是根据相关性大小把变量分组,使组内相关性较高,组间相关性较低,每组变量代表一个基本结构,这个基本结构叫公共因子。对于由多指标构成的某问题可试图用最少个数的公共因子的线性函数与特殊因子之和来表示每一个分量,并且要求各因子之间相互独立。这样不仅消除了指针间信息重迭,而且还起到了降维的作用,便于抓住事物的主要矛盾。
　　 因子分析模型如下:

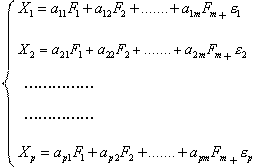
    可简写为: X=AF+ε

    其中A=  F =(F1,F2…,Fm),ε=(ε１,ε２ ,。。。εＦ)

    模型中X1,X2 ,。。。XP是p个原指标;A为因子载荷矩阵;F1,F2。。。。。Fm叫公共因子(也称主因子),主因子在原指标的表达式中是共同出现的,是相互独立的不可观察的理论变量,其含义要根据实际问题与分析结果而定, ε１,ε２ ,。。。εＦ叫特殊因子,是各指标Xi所特有的因子,各特殊因子之间以及与所有公共因子之间也是相互独立的,叫因子负荷,其数量意义是:

    （1）表明X1与Fi的相依程度,该系数越大,相依程度越高。

    （2）表示指标Xi对F的每一个分量F1,F2。。。。。Fm的共同依赖程度。若接近于Xi的方差,则可直接用F1,F2。。。。。Fm的线性组合来表示Xi而忽略特殊因子ε。
    求解因子模型的关键是求解因子负荷系数。求解因子负荷系数的方法有主成份分析法、广义最小平方法、极大似然法等,最常用的是主成份分析法。
　　以上是因子分析法的一般原理和基本的分析计算步骤。在实际运作过程和实务中,可利用SPSS、SAS等多变量经济数据分析软件进行非常方便地操作。
　　 3、指标权重的确定
　　指标权重的确定的方法有主观赋权法,客观赋权法。主观赋权法是根据各指标的实际观察值所提供的信息大小来确定各指标的权重，一般使用于综合评价指标数目较少,各指标对综合评价值确定的重要性易于区别并且各指标间相关性较小的情况下。当指标的重要性很难区分时可采用客观赋权法，即利用各指标实际观察值所提供的信息量大小来确定指针权重,提供信息越多的指针赋权重就越大, 反之所赋权就越小。本文采用客观赋权法――巴特莱特法来估计因子得分。
　　 4、景气指数的生成：
    设公因子 F1,F2。。。。。Fm的估计值即因子得分为 ……,各公因子的特征值分别为   ……,根据特征值的贡献率构造综合得分为:

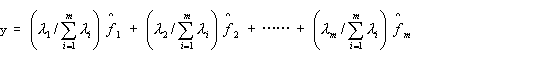
    可见各公因子综合景气指针的信息,而y是综合 ……各因子信息,并以贡献比率为权,称y为景气指数。